Kepler's 2nd

Post Reply New Topic

I thought I'd start here and suggest these things about Euclidean geometries (and in local regions of manifolds where such geometries roughly hold):

• The specific area swept per unit time, in the presence of centrally directed forces, is a function of initial conditions and it doesn't matter if the centrally directed force is zero, negative, positive, or some arbitrary real function of time -- in other words, so long as gravity was a central force between particles, it was an inescapable consequence that Kepler discovered and not some special case due to the particular equation that Newton would later develop.
• This is an 'if and only if' situation of equivalence, so in cases where equal areas are swept in equal times, all acceleration must be therefore be centrally directed and there cannot be any non-zero transverse acceleration. Which leads towards the idea of conservation of angular momentum.

Look at the following diagram of an orbit. (I've used an ellipse, but it's not necessary to assume one here. It's included just as an aid in keeping hold of the idea of orbits, generally. The important detail is only the origin I'm using, for now, which is centered on one of the two particles involved.)

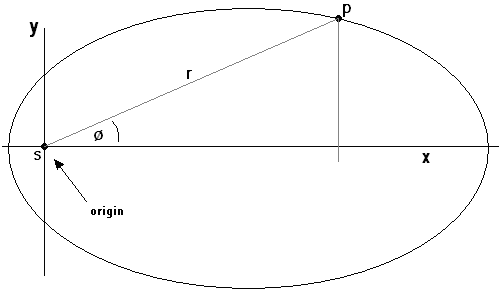
The equations relating the two indicated ways of specifying the position of 'p' are:


We could use a basis vector approach to analyze the relationships, but instead I'll just use straight calculus to get to the same place:


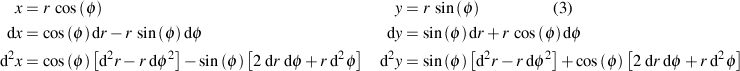
We're going to take a look at things from a radial/transverse point of view, which is why I'm going to this trouble here. Does this make sense, so far?

Jon

Okay. I guess I'll take it slower. Let's just make sure that the first derivative steps are laid out and understood. If we can agree that far, I'll go through the 2nd derivative in painstaking detail to show how I arrived at the result.

One thing to keep in mind that I'm not taking the derivative with respect to anything, in particular. As long as what that thing is will turn out later to be independent, it doesn't matter. We can just inject it in, when we feel like it, without affecting these steps here. If this feels somehow uncomfortable, say so.

For x:


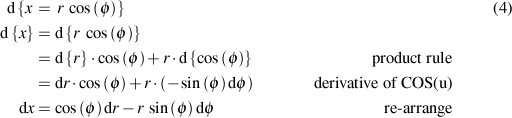
This reads as "any infinitesimal change in x is equal to the cosine of the current angle times a corresponding infinitesimal change in r minus r times the sine of the current angle times a corresponding infinitesimal change in the current angle. Which if you think about it makes sense. Any finite value times an infinitesimal is just another infinitesimal, clearly, merely scaled by the finite value. So the sum of products, each of which are infinitesimals themselves, will just be another infinitesimal. Nothing shocking about that.

For y:


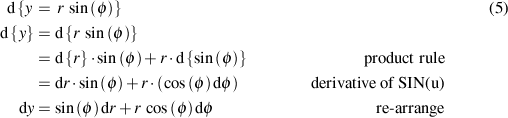
This reads as "any infinitesimal change in y is equal to the sine of the current angle times a corresponding infinitesimal change in r plus r times the cosine of the current angle times a corresponding infinitesimal change in the current angle. Which if you think about it also makes sense.

Are we on the same page, now, regarding at least the first derivative??

Jon

I hope I'm not losing lau and wolphin on this. This is what I meant when I talked about the use of infinitesimals in a context that is just slightly different that the usual exposition found and I thought I'd just jump in and see how it goes.

I guess I could say things a little differently about calculus and see if that helps...

Almost every calculus book includes on its inside cover flaps some examples of common derivatives and integrals.

I'll take one of the examples and set it up as equation (6) and then work through the details to get to the way I prefer to "see" it:


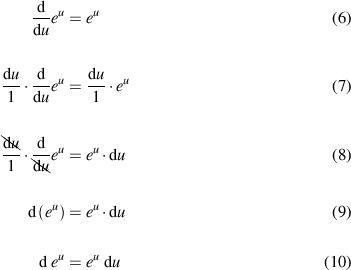
Equation (9) shows the basic idea for this. The d() is an operator. It operates on some function. The result is a finite value times an infinitely small value held in the special variable called du. In this sense, calculus is just algebra with one added thing -- a new variable type that can only hold infinitely small values. We indicate these variables by prefixing 'd' to them so we can easily find them and recognize them. But they are just variables, no different from other finite value variables usually found in algebra. We can cancel them, multiply them, take their ratios, and so on. In fact, when you see dx/dt=4, that just means that the infinitesimal value held in dx is 4 times larger than the infinitesimal value held in dt. It's just a comparison of two values and such comparisons can readily produce finite values, even though they are each, themselves, infinitely small values. I might just as well have written dx = 4*dt.

(Interestingly enough, one can actually raise e to the power of that d() operator, without anything inside it -- just the operator itself and alone. In fact, that particular one is an important concept about making observations of reality. But that is a segue into operator calculus and interpreting discrete observations of a supposed continuous process and another subject.)

Equation (10) just drops the explicit multiplication shown in (9) and removes the parentheses on the left hand side. But that doesn't change the meaning. 'd' is still an operator function and the result is still just the same product shown in (9) and not some matter of end irons or bookends. This is still algebra, really, with functions and variables and expressions. Just a new variable kind added in, that's all.

I guess I'm going back to this because I'm worried. Let me know.

Jon

I'm with you, I just ducked out of sight for a day or two to work on some assignments.

So, the "infinitesimal analysis" point of view isn't necessarily one that's widely seen. Personally, I would have just made everything a function of an arbitrary parameter t (or if time will be used later for something different, s) since that's just what is essentially implied here anyways. But I'll bear through it

Ah, but it doesn't need to be time. Any variable that's independent can later be used. Or never, at all, in fact. The statements stand accurately without ever using another variable to compare with and show the relationships between the indicated infinitesimals, without any time or other process variable being introduced. They are quite useful, in fact, without time in situations where you are merely looking at geometric relationships alone. If I'd taken this from a basis vector approach, you'd see this fact, abundantly. You want me to do that, instead? It shows the same relationships of the basis vectors as I just derived in (3) and if you look at that, you will know firmly why time not only isn't needed by why conflating or confusing it into the statements actually makes them worse and less practical.

This is the more powerful way of seeing it.

And there is broader use, not tying it down, as suggested in operator calculus. But for here and now, yeah, it's close enough to make no never mind and if that helps, go for it.

Anyway, I can point to chapter and verse in mathbooks that say that the chain rule isn't about cancelling variables even though it looks like you can and then they also go on, without example, to say to avoid thinking that way. However, it was the original way of seeing things (Newton's fluxions, for example) and flummoxed mathematicians because it gave the right answers but hadn't yet been grounded properly in mathematics. It was Dedekind and Weierstrass who did that with limit concepts and avoided the idea that actual infinitesimals might exist at all, but really it took yet another 100 years for Robinson to discover the original ideas were rigorous, too, and that you could develop a field founded upon the actual concept.

I just prefer the old way of seeing it.

Jon

Okay. So here is a slight modification of the orbit. Again, the ellipse isn't necessary. It could be a corkscrew, for all I care. It's just there because it sometimes helps to think that way, but it isn't crucial.


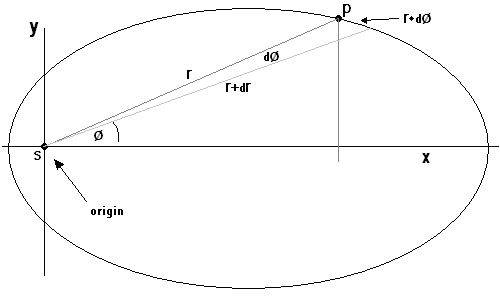
In this, I've allowed the planet/particle to sweep out a small area in a change in position. The area swept out is:


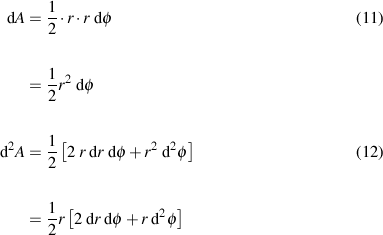
Here, you may now take note that there is a term in equation (2) here, quite similar to one found in a few places in equation (3).

Okay. So you brought up time. Might as well decide now to introduce the idea. Time is assumed independent of space, so we can just add it. Let's start with the rate and acceleration of area change per unit time in equations (11) and (12):


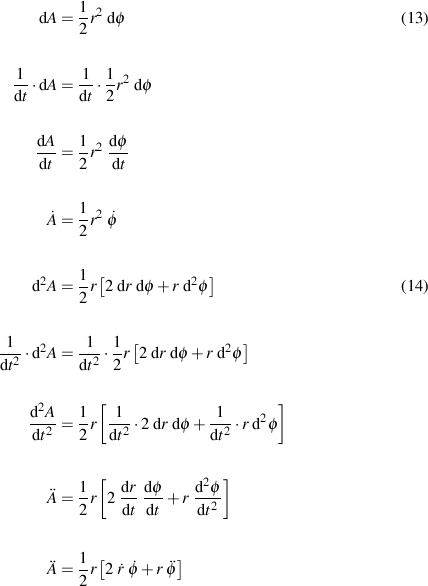
And then do the same for the last pair in equation (3):


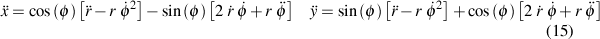
Okay, now let's look at some arbitrary acceleration on the particle/planet. We won't assume any particular direction for it, so I will actually show it pointing clearly in the "wrong" direction, just to make the point clear. In the following image, I've superimposed an arbitrary acceleration vector on the planet/particle. It's 'a'. There are two possible ways I've suggested in viewing the components to it: (ax,ay) and (ar, at).


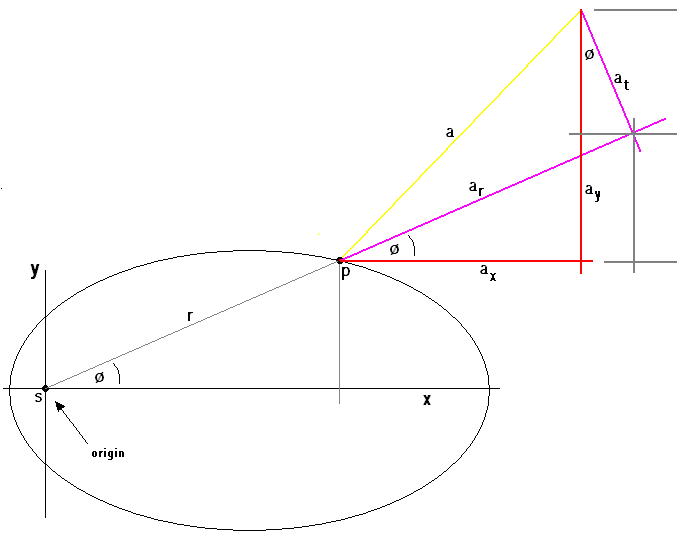
Their relationship, from simple geometry, is: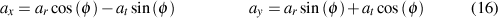

If you examine the picture I've drawn, I think you should be able to work through the various right-triangles to see where these come from. If you can't, just let me know. Basically, it's just a rotation. And I hope the picture helps see the details and lets you double check my work.

It's clear that: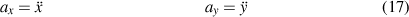

So, by inspection in comparing equation (15) and (16), you should be able to see that:


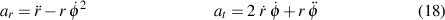
At this point, it should be clear from looking at the final version of equation (14) that the rate of change of area is only dependent upon the the transverse acceleration and has NOTHING whatever to do with the magnitude of the radial acceleration. When Kepler noted "equal areas in equal times" he was just saying that the final version of equation 14 equals zero. And since 'r' is not necessarily zero, the only other way that happens is if the transverse acceleration is always zero. And this implies that all acceleration must be radial -- gravity must be central, in effect.

But another point here is that it doesn't matter whether the central acceleration is negative, positive, or zero. So long as the transverse acceleration is zero, equal areas will always be swept out. If gravity didn't exist and a particle went in a straight line by a star or sun, it would still sweep out equal areas. If you were in a rocket ship and either pointed your rocket engines towards or away from the sun and no matter how you varied your thrust over time, so long as all your acceleration was lined up centrally, you would sweep out equal areas in equal times.

It simply doesn't matter what exact force, attractive, repulsive, time-varying in some odd way, or zero -- so long as there was no transverse acceleration to particle motion in orbits, the law of equal areas would have had to have been observed. It's not a special case of some specific attraction equation. It's fundamental to any central-only force, constant, varying, or otherwise.

The reverse is also true. If you observe equal areas in equal times being swept, you know there is no transverse acceleration or force acting on the particle. All must be radial. In two particles of equal mass and equal distance from a center, opposite to each other and rotating attached in a fixed way to their center so that the forces cancel, the net force is always zero, there can be no transverse acceleration as a result, and equal areas must be swept in equal times, no energy is consumed (net force is zero, no matter the distance), and angular momentum therefore must be conserved.

Jon

Now, if you think about the above a little, and in particular consider the case where the force/acceleration due to gravity is zero and a particle simply follows a line at a constant velocity, and if you also embrace the idea that the area swept per unit time is constant even under central accelerations, it becomes pretty clear that the only thing that determines the area being swept is the particle's position and velocity vector at any instant you choose. If there is some particle at some observed position and if you know it's velocity vector at that point, you know the value of this constant and it will not change.

In orbital mechanics, the term for it is the "areal constant" and its value is, by convention, taken to be twice that of the value in equation (13), or:


It's an important value in orbital mechanics and has a constant value for any planet in orbit about one star (and where you can effectively ignore the impacts of other gravity influences or forces.)

Jon

Sure, it all seems to make sense.

I do feel compelled to point out that using vectors (along with assuming angular momentum is conserved), everything shrinks down into a couple lines: namely, observing that (using an infinitesimal-style argument like yours):

R be the position vector of the particle, dR the infinitesimal displacement vector, and dA be the area swept out

dA = (1/2) * | R x dR | (by a vector identity)

dA = (1/2) * | R x (dR/dt)*dt | = (dt) * (1/2) * | R x (dR/dt) | (since dt is a "scalar" infinitesimal)

letting P be the vector momentum of the particle and observing that P = (m)*(dR/dt):

dA = (dt) * (1/2m) * | R x P |

(dA/dt) = (1/2m) * | R x P |

Then observing that | R x P | is simply the definition of angular momentum, and that both angular momentum and mass are constant, dA/dt is constant as well and so equal areas are swept out in equal times.

Note that since the only assumption was that angular momentum is conserved, this holds as long as the net torque on the particle in question is zero, which is equivalent to what you said about no tangential force.